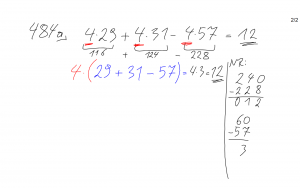M1f – Video „Quader Kanten“
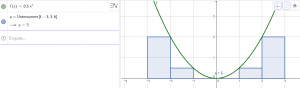
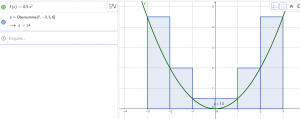
M72 – Integralrechnung Ober- und Untersumme
Siehe auch:
dynamisches Arbeitsblatt Unter- und Obersumme
M1f – Herausheben
WMA01-Folgen
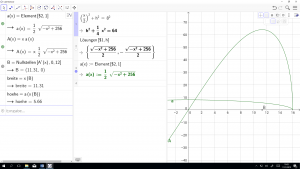
M71-Umkehraufgaben S.116+Bspl. 260
Das Einstiegsbeispiel auf S.116,117:
Weiterlesen
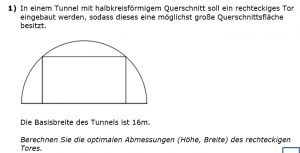
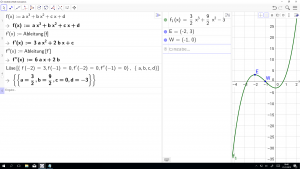
M71-Extremwertbeispiel 2.Schularbeit
M62 – Winkelfunktionen: Bogenmaß, Symmetrie und Periodizität
Bogenmaß
Einheit: Radiant (rad)
Eine volle Umdrehung (360°) entspricht 2*pi
Umrechnung von Grad in Bogenmaß: b=a*pi/180 (a … Winkel im Gradmaß, b … Winkel im Bogenmaß)
Umrechnung von Bogenmaß in Gradmaß: a=b*180/pi (a … Winkel im Gradmaß, b … Winkel im Bogenmaß)
Hinweis: Wendet man Winkelfunktionen im Taschenrechner im Bogenmaß an, muss man auf RAD statt DEG umschalten!
Sinusfunktion
Symmetrie: Punktsymmetrisch sin(x) = -sin(-x)
Periodizität: Periodenlänge = 2*pi
sin(x) = sin(x+k*2*pi), wo k aus Z.
Cosinusfunktion
Symmetrie: Axialsymmetrisch: cos(x) = cos(-x)
Periodizität: Periodenlänge = 2*pi
cos(x) = cos(x+k*2*pi), wo k aus Z.
Tangensfunktion
Symmetrie: Punktsymmetrisch tan(x) = -tan(-x)
Periodizität: Periodenlänge = pi
tan(x) = tan(x+k*pi), wo k aus Z.
undefinierte Stellen = Polstellen: da tan(x) = sin(x)/cos(x) sind die undefinierten Stellen dort, wo der cos(x)=0 ist.
![]()
M1f – Distributivgesetz (Tafelbilder)
Tafelbilder „Distributivgesetz“